Local Intrinsic Dimension Estimation
1 Introduction
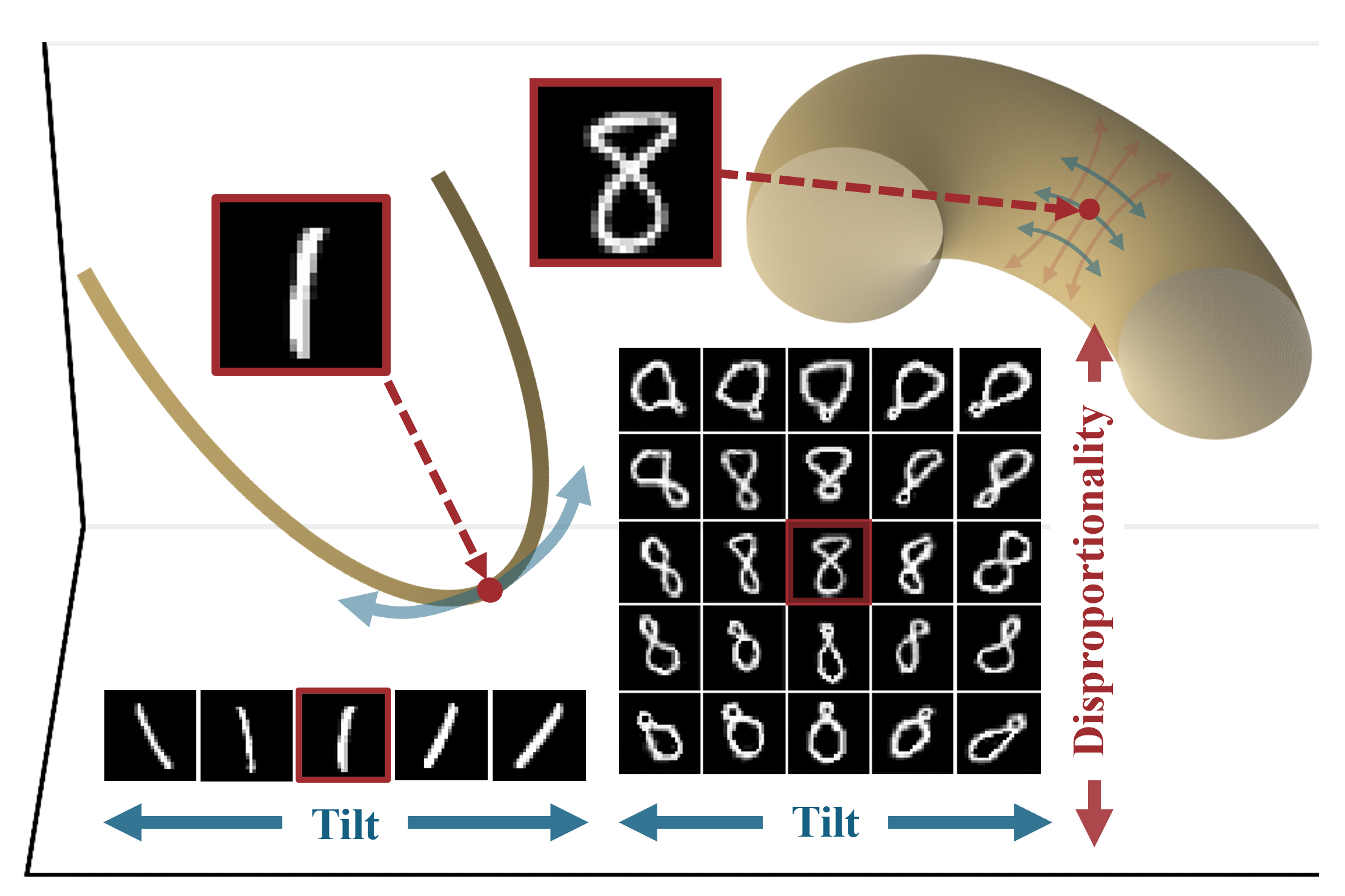
High-dimensional data in deep learning applications such as images often resides on low-dimensional submanifolds, which makes learning the properties of the learned manifold by a generative model a relevant problem (Loaiza-Ganem et al. 2024). One of the most important properties of a manifold is its intrinsic dimensionality which can loosely be defined as the number of factors of variation that describe the data. In reality, rather than having a single manifold representing the data distribution, we have a collection of manifolds (Brown et al. 2023) (or more recently the CW complex hypothesis (Wang and Wang, n.d.)) that describe the data distribution. Intuitively, this means that for example for a dataset of MNIST digits, the manifold of 1s and 8s are different, and they might have different intrinsic dimensionalities. Therefore, instead of (global) intrinsic dimensionality, we are interested at local intrinsic dimensionality (LID) which is a property of a point with respect to the manifold that contains it.
Various definitions of intrinsic dimension exist (Hurewicz and Wallman 1948), (Falconer 2007), (Lee 2012), we follow the standard one from geometry: a d-dimensional manifold is a set which is locally homeomorphic to \mathbb{R}^d. For a given disjoint union of manifolds and a point x in this union, the of x is the dimension of the manifold it belongs to. Note that LID is not an intrinsic property of the point x, but rather a property of x with respect to the manifold that contains it. Intuitively, \text{LID}(x) corresponds to the number of factors of variation present in the manifold containing x, and it is thus a natural measure of the relative complexity of x, as illustrated in Figure 1.
Computing the LID for a given point is a complex task. Traditional non-parametric (or model-free) methods, such as those in the skdim-library (Bac et al. 2021), are computationally intensive and not scalable to high-dimensional data. Consequently, there is growing interest in using deep generative models for LID estimation. This approach is valuable not only for understanding the data manifold but also for evaluating the generative model itself. Discrepancies between the model-implied LID and the ground truth can highlight model deficiencies and help us to improve the quality of generative models. Here, we thoroughly explore LID methods for deep generative models with a particular focus on score-based diffusion models (Song et al. 2021), and explore their applications in trustworthy machine learning.
2 What is LID Used For?
LID estimates can be interpretated as a measure of complexity (Kamkari, Ross, Hosseinzadeh, et al. 2024) and can be useful in many scenarios. These estimates can also be used to detect outliers (Houle, Schubert, and Zimek 2018) (Anderberg et al. 2024) (Kamkari, Ross, Cresswell, et al. 2024), AI-generated text (Tulchinskii et al. 2023), and adversarial examples (Ma et al. 2018). Connections between the generalization achieved by a neural network and the LID estimates of its internal representations have also been shown (Ansuini et al. 2019), (Birdal et al. 2021), (Magai and Ayzenberg 2022), (Brown et al. 2022). These insights can be leveraged to identify which representations contain maximal semantic content (Valeriani et al. 2023), and help explain why LID estimates can be helpful as regularizers (Zhu et al. 2018) and for pruning large models (Xue et al. 2022). LID estimation is thus not only of mathematical and statistical interest, but can also benefit the empirical performance of deep learning models at numerous tasks.
3 Useful links
For a guide on how to use our LID estimators, check out our notebook. We are also planning to release our latest work on using the Fokker-Planck equation of diffusion models to estimate LID, which we call FLIPD. When posted, it will show up here.