Out-of-Distribution Detection and the Likelihood Paradox
1 Introduction
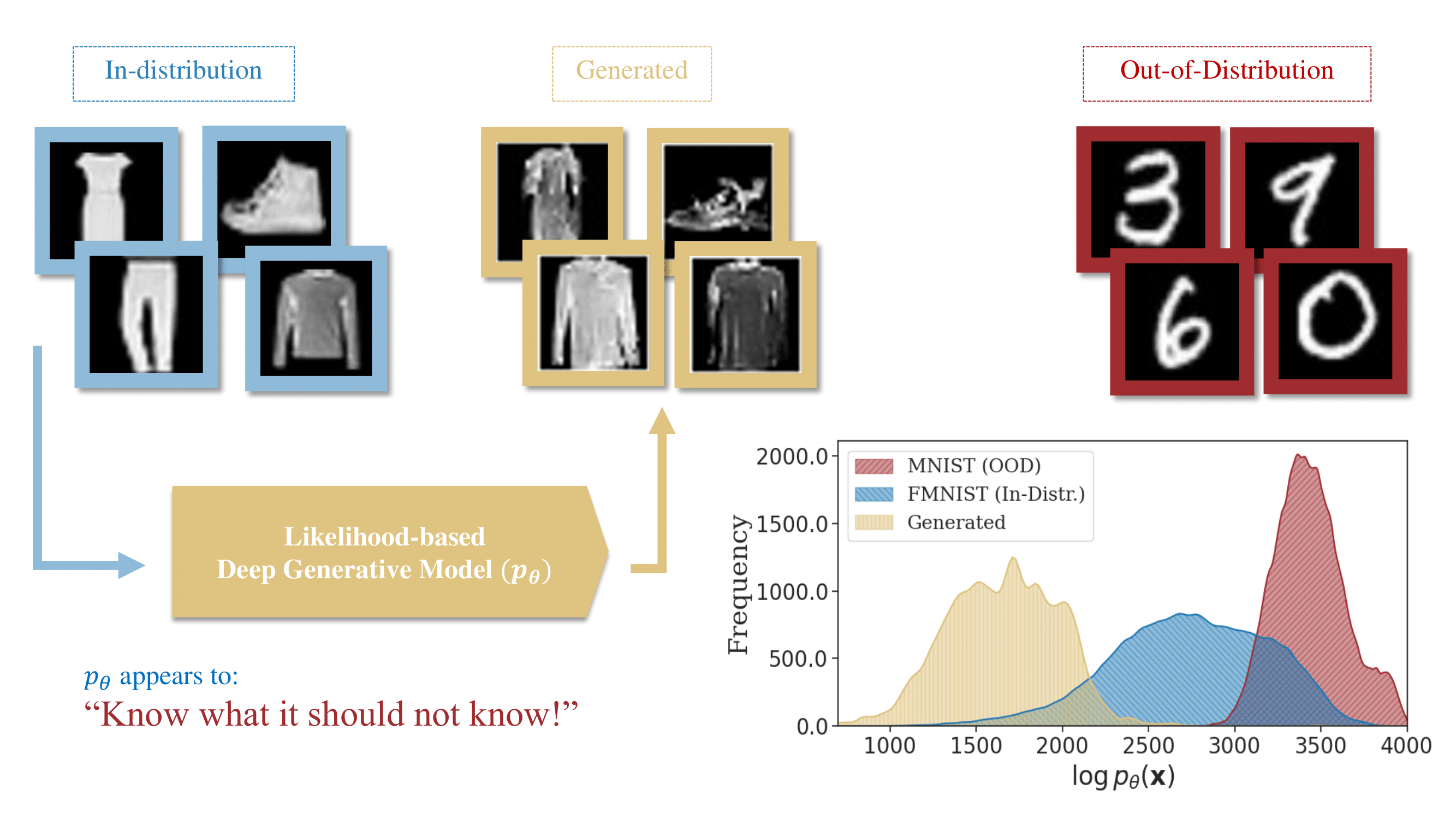
Intuitively, when one trains a likelihood-based generative model, it implicitly or explicitly increases the likelihood for the training (in-distribution) data. Therefore, it is reasonable to assume that since the likelihoods integrate to zero (likelihoods are in fact a valid probability density p_\theta) out-of-distribution (OOD) data would obtain low likelihoods. However, paradoxically, deep generative models do not show this behaviour. In fact, based on the research presented in “Do deep generative models know what they don’t know?” (Nalisnick et al. 2019), OOD datapoints sometimes consistently get assigned higher likelihoods than in-distribution data. This phenomenon, which is coined the Likelihood Paradox, is not only a significant challenge for OOD detection, but also a fundamental question about the nature of deep generative models. Figure 1 illustrates this phenomenon for a generative model, whereby the model is trained on FMNIST but assigns higher likelihoods to MNIST digits (in red) that it has never seen before! Adding to the perplexity, the model never generates things that are even remotely similar to MNIST digits, as depicted in Figure 1.
In our study (Kamkari, Ross, Cresswell, et al. 2024), we facilitate the simple observation that while generative models assign high probability density to OOD data, the probability mass assigned to the OOD manifold is almost zero. Otherwise, the model would sometimes generate OOD datapoints, which is not the case. In turn, rather than relying on likelihoods alone, we should use extra informatioin that reveals characteristics of the probability mass. For example, when OOD data is supported on an extremely low-dimensional manifold, then no matter how high the probability density is, the probability mass assigned to the OOD manifold is almost zero. This observation is the basis of our proposed method, which we call Out-of-Distribution Detection with Local Intrinsic Dimensionality (OOD-LID).
2 A Cartoon Illustration
Our explanation for the likelihood paradox is as follows: While paradoxical out-of-distribution regions might exist due to the complexity of deep generative models, the fact that the model never generates them indicates that they must have low probability mass. Calculating probability mass directly is intractable for complex regions in high-dimensional spaces. Instead, we can intuitively think of the probability mass as the volume of the region multiplied by the probability density. Although computing the volume of a small region too is challenging, we establish that this volume is monotonically related to the intrinsic dimensionality of the region, for which we have estimators.
Therefore, we propose using the intrinsic dimensionality of the region as a proxy for its probability mass. When a manifold has lower intrinsic dimensionality than another, its volume is infinitely smaller, and thus, its probability mass is also infinitely smaller. Drawing an analogy, we hypothesize that these paradoxical likelihood regions lie on lower-dimensional manifolds. Consequently, even though the probability density might be high, the probability mass is infinitely small.
We have illustrated our point in Figure 2. The cartoon shows a model trained on FMNIST and assumes FMNIST lies on a higher-dimensional manifold (in blue) than MNIST (in red). The model assigns higher likelihoods to MNIST digits, which are OOD, but because the volume of the MNIST region is infinitely smaller due to its lower intrinsic dimensionality, the probability mass assigned to the MNIST manifold is almost zero. Therefore, the model never generates MNIST digits.
Leveraging this observation, we design a simple yet effective OOD detection algorithm: estimate both the likelihood and intrinsic dimensionality for each datapoint and classify a datapoint as in-distribution if and only if both the likelihood and intrinsic dimensionality are high (above certain thresholds \psi_{\mathcal{L}} and \psi_{\text{LID}_\theta} on likelihood and LID, respectively). As depicted in Figure 2, this method will (1) classify pure noise as OOD because it has low likelihood, (2) classify MNIST as OOD because despite having high likelihood, it has low intrinsic dimensionality, and (3) classify FMNIST as in-distribution because it has both high likelihood and high intrinsic dimensionality.
3 Relation to Prior Work
Prior work have shown that the paradox is one-sided, meaning that when training a model on dataset A and evaluating it on dataset B, the model assigns higher likelihoods to B than A only if A is more complex than B Caterini and Loaiza-Ganem (2021). This means that if we train a model on MNIST digits and evaluate it on FMNIST digits, the model assigns higher likelihoods to MNIST.
We argue that LID here can be thought of as a measure of complexity! In fact, we have a new paper dedicated to this topic (Kamkari, Ross, Hosseinzadeh, et al. 2024). When the likelihood paradox happens, while likelihood cannot reliably distinguish between in-distribution and OOD data, LID can.
4 Why Does the Paradox Happen in the First Place?
Our work explains why the model never generates OOD data, despite assigning high likelihoods to it. However, the question of why this paradox occurs in different generative models has been explored in the literature. For example, (Kirichenko, Izmailov, and Wilson 2020) and (Schirrmeister et al. 2020) argue that the inductive biases of the networks used for generative modeling are the culprit. These networks tend to over-fixate on high-frequency patterns in the images, leading them to assign high likelihoods to all natural images, regardless of whether they are in-distribution or OOD. In fact, due to simplicity priors discussed in (Caterini and Loaiza-Ganem 2021), the model may assign higher likelihoods to OOD data than to in-distribution data.
Thus, we see our explanation as complementary to these works. While they explain why the model assigns high likelihoods to OOD data, we provide an explanation for why the model never generates OOD data. We use this observation to design a new OOD detection algorithm.
5 How to Use Our Method?
We have provided a hands-on guide to get started with our method here. Please cite our repository and paper using the following:
@misc{dgm_geometry_github,
author = {Hamidreza Kamkari, Brendan Leigh Ross, Jesse C. Cresswell, Gabriel Loaiza-Ganem},
title = {DGM Geometry},
year = {2024},
howpublished = {\url{https://github.com/layer6ai-labs/dgm_geometry}},
note = {GitHub repository},
}
@article{kamkari2024oodlid,
title={A Geometric Explanation of the Likelihood OOD Detection Paradox},
author={Kamkari, Hamidreza and Ross, Brendan Leigh and Cresswell, Jesse C and Caterini, Anthony L and Krishnan, Rahul G and Loaiza-Ganem, Gabriel},
journal={arXiv preprint arXiv:2403.18910},
year={2024}
}